Principio di funzionamento di un oscilloscopio
Esistono due grandi
famiglie di oscilloscopi: quelli analogici e quelli digitali. Gli oscilloscopi
analogici sfruttano un principio di funzionamento piuttosto semplice, basato sul
particolare pilotaggio del loro tubo catodico. Le griglie dell'asse Y del CRT
sono pilotate dal segnale di ingresso che si desidera mostrare, mentre le
griglie dell'asse X sono pilotate da un generatore a dente di sega con frequenza
impostabile dall'utente (la base dei tempi). Il dente di sega fa procedere il pennello a velocità costante lungo l'asse orizzontale,
da sinistra verso destra; nel mentre le variazioni del segnale fanno salire o
scendere il pennello, che così disegna l'andamento del segnale in
funzione del tempo. Questa operazione è ripetuta per ogni dente di sega; sul
video si sovrappongono tante "spazzolate", che grazie alla persistenza
dei fosfori dello schermo (e delle immagini sulla retina) formano un'immagine.
Per mostrare in modo stabile un segnale periodico è necessario che tutte le
spazzolate si sovrappongano perfettamente fra di loro, il che equivale a dire
che la frequenza del dente di sega deve essere un multiplo o sottomultiplo della
frequenza del segnale periodico; questo si può ottenere agendo manualmente
sulla regolazione fine della base dei tempi, oppure utilizzando un particolare
circuito (detto "trigger") che permette di sincronizzare i denti di
sega direttamente con il segnale di ingresso.
Questa è una descrizione
molto grossolana del funzionamento di un oscilloscopio analogico, che ho fatto
soltanto per farvi notare come in effetti in questi strumenti il segnale in
ingresso sia completamente tracciato sullo schermo. È solo per una
limitazione dei fosfori del CRT, del nostro occhio e ovviamente del nostro
cervello che non possiamo "percepire" l'intero segnale in maniera
continua, in tutta la sua evoluzione temporale.
Gli oscilloscopi digitali
sono diversi proprio in questo. In un oscilloscopio digitale il
segnale in ingresso viene campionato da un ADC, memorizzato e mostrato in un
secondo tempo su un display. Non c'è un CRT da
aggiornare continuamente, la scheda video che pilota il monitor o l'LCD è in grado di mantenere le immagini mostrate
per un tempo indeterminato. E anche se si volesse, un LCD non potrebbe reggere
le frequenze di scansione orizzontale tipiche di un oscilloscopio analogico
(decine o centinaia di MHz): al massimo si parla di frequenze di aggiornamento
di qualche decina o centinaia di Hz.
Tutto ciò ha un'implicazione molto importante: gli oscilloscopi digitali in
genere mostrano soltanto una "fetta" dell'evoluzione temporale di un
segnale. Per noi umani non c'è differenza, tanto non riusciremmo comunque a
vedere dei fenomeni della durata di microsecondi "in tempo reale".
Ciò determina però una caratteristica importante del funzionamento
dell'oscilloscopio digitale: esso non deve limitarsi a mostrare quanto più
segnale possibile su schermo, ma può decidere con relativa calma quali fette mostrare,
in quale ordine e con quale combinazione.
Queste scelte sono ciò
che distinguono i vari tipi di oscilloscopio digitale. Non è mia intenzione
fare una trattazione approfondita dell'argomento; per questo trovate degli
articoli molto interessanti su Internet, ad esempio questo articolo
su EDN. Io mi
limiterò a descrivere le due architetture fondamentali.
Il primo tipo è quello
più intuitivo, che fa semplicemente ciò che ho descritto in
precedenza: campiona una fetta di segnale a una certa frequenza
e la mostra su schermo a intervalli stabiliti. Questi intervalli sono
automaticamente allungati o accorciati da un circuito di trigger (questa volta
costituito da logica digitale) in modo che i segnali periodici siano mostrati in
maniera stabile sullo schermo:

Come sempre vale il
teorema del campionamento di Nyquist: se ciascuna fetta viene campionata ad
esempio a 10 MSPS (milioni di campioni al secondo), potremo ricostruire al
massimo fino alle componenti spettrali a 5 MHz del segnale. Nel caso che ci
siano componenti a frequenza superiore esse creeranno degli alias a
frequenze più basse, e noi vedremo segnali che in realtà non esistono.
Un oscilloscopio di questo
genere è caratterizzato quindi da una banda passante pari alla metà della
frequenza di campionamento dei suoi ADC; tutto ciò che è al disopra di queste
frequenze deve essere filtrato ancora prima di entrare nell'ADC.
Il secondo tipo di
oscilloscopio è quello che
sfrutta la tecnica dell'equivalent time sampling, o ETS. Ormai tutti gli oscilloscopi
professionali funzionano così; questa tecnica permette di ricostruire componenti a frequenza molto
più alta di quella di campionamento degli ADC, anche di un ordine di grandezza
e oltre.
Come si spiega questa apparente profanazione del teorema di Nyquist? Se guardate
la figura precedente potrete farvi un'idea. In quel caso le fette
vengono lette a intervalli di tempo doppi rispetto al periodo del segnale;
in teoria avremmo potuto leggere ogni periodo, quindi
abbiamo buttato via metà del contenuto informativo che potevamo sfruttare. In
realtà i segnali che si leggono su un oscilloscopio hanno una frequenza molto
superiore a quella di refresh dello schermo, quindi le letture scartate diventerebbero migliaia o milioni anziché una su due. L'oversampling sfrutta
questo principio, ricostruisce la forma d'onda in più
passate "fotografandola" ogni volta in un punto diverso:
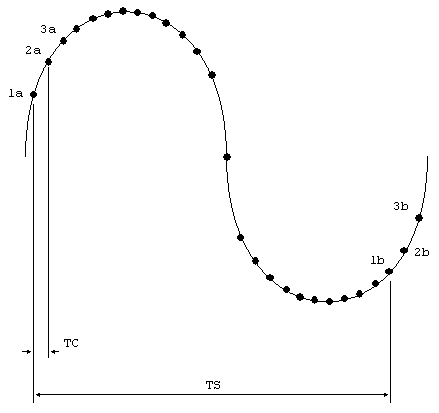
Supponete che quello in
figura sia un singolo periodo del nostro segnale e TS sia il tempo di
campionamento dell'ADC utilizzato. Come si vede TS è maggiore della
metà del tempo di un periodo, per cui il principio di Nyquist non è
soddisfatto e anche se il segnale fosse perfettamente sinusoidale non
riusciremmo a campionarlo con il metodo "tradizionale". Campioneremmo
quindi il punto 1a e 1b e da essi non riusciremmo a ricostruire il segnale
originale.
Con l'ETS sfruttiamo invece più periodi consecutivi e
"trasliamo" ogni volta la lettura di un tempo molto più breve di
quello di campionamento; nella figura ho chiamato questo tempo TC. Nel primo
periodo leggeremo i punti 1a e 1b, nel secondo periodo i punti 2a e 2b, nel
terzo periodo i punti 3a e 3b e così via. Mettendo assieme tutte queste letture
è possibile ricostruire il segnale periodico anche se esso ha componenti
spettrali a frequenza molto più alta di 1/(2TS).
La tecnica dell'ETS
è un trucco che permette di sfruttare porzioni temporali del
segnale che altrimenti non sarebbero mostrate per aumentare la banda passante
percepita. Dato che il segnale viene ricostruito in più letture, la tecnica funziona solo ed esclusivamente per i segnali periodici;
è per questo motivo che molti degli oscilloscopi digitali da centinaia o migliaia di
MSPS hanno delle prestazioni molto più modeste
per quanto riguarda la visualizzazione dei transitori e degli eventi non
ripetitivi in generale. Provate a fare una lettura con trigger "one-shot"
sul vostro mirabilante oscilloscopio da 500 MSPS, e vedrete come esso magicamente
si trasformerà in un oscilloscopio molto più modesto...
Ci sono diverse
tecniche per ovviare a questo problema; la più comune è quella di sfruttare
gli ADC dei canali eventualmente non utilizzati. Se ad esempio abbiamo a nostra
disposizione quattro ADC per leggere un singolo canale, basterà
"traslare" il clock di ciascuno di essi di un tempo pari a TS/4 e
farli lavorare assieme in modo "interlacciato". In questo modo la
frequenza di campionamento sarà quadruplicata, e ciò varrà anche per i
segnali non periodici. Gli oscilloscopi digitali di punta sfruttano entrambe
queste tecniche (ETS e riassegnamento di ADC non utilizzati).
Di che tipo sarà il
nostro oscilloscopio? Presumibilmente del primo tipo (senza ETS).
Questa tecnica non è difficilissima da implementare, ma richiede elettronica
più complessa; inoltre ormai si trovano degli ADC da decine di MSPS a un prezzo
ridottissimo, e ritengo che per un hobbista già avere un oscilloscopio da 20-30
MHz sia in molti casi sufficiente. Poi è sempre il solito discorso: se volete
di più probabilmente siete anche disposti a spendere di più, e al disopra di
una certa soglia non ha più senso autocostruirsi le cose.
Indice
(precedente) Introduzione e premesse
(prossimo) Schema
a blocchi
|